Introducción

Los sistemas de reconocimiento de dígitos manuscritos en aplicaciones móviles o procesos bancarios automatizados funcionan mediante algoritmos de aprendizaje automático, específicamente redes neuronales artificiales. Estos sistemas procesan información visual mediante modelos matemáticos entrenados para identificar patrones numéricos.

Este análisis examina el proceso computacional mediante el cual las redes neuronales identifican dígitos manuscritos, utilizando como base el conjunto de datos MNIST (Modified National Institute of Standards and Technology). Este set de datos contiene aproximadamente 70,000 muestras de imágenes en escala de grises de 28×28 píxeles, organizadas en 10 categorías correspondientes a los dígitos del 0 al 9.

Veremos cómo una red neuronal:

1. Transforma una imagen en números que puede procesar.
2. Detecta patrones jerárquicos, desde bordes simples hasta formas complejas como bucles y trazos.
3. Toma decisiones calculando probabilidades para cada dígito (¿es un «3» o un «8»?).

Además, incluiremos una explicación técnica con fundamentos matemáticos y código en Python para quienes deseen profundizar en la implementación práctica. Descubriremos cómo se ajustan los parámetros del modelo durante el entrenamiento y cómo evitar problemas como el sobreajuste.

Si alguna vez te has sentido intrigado por cómo las máquinas «ven» y «clasifican» imágenes, ¡esta entrada es para ti! 

Reconociendo números escritos a mano – nivel divulgativo

Para ilustrar cómo funciona una red neuronal, tomaremos como ejemplo el problema del reconocimiento automático de dígitos manuscritos. Los datos para éste estudio han sido extraídos de la base de datos del Modified National Institute of Standards and Technology (MNIST). La MNIST es una extensa colección de base de datos que se utiliza ampliamente para el ajuste de parámetros de diversos sistemas de procesamiento de imágenes. Este es un clásico en el mundo del aprendizaje automático, y se basa en imágenes de 28×28 píxeles que representan números del 0 al 9.

Entrada de Datos (Capa de Entrada)

La imagen del número se convierte en un vector de 784 valores (28 × 28 píxeles). Cada valor representa la intensidad del color en un píxel, normalizado entre 0 y 1. Esta será la información que alimentará a la red neuronal.

Procesamiento Interno (Capas Ocultas)

Las capas ocultas de la red realizan el trabajo de interpretación de esta información. Cada capa aplica una transformación matemática sobre los datos de la capa anterior.

En las primeras capas:

• Se detectan patrones simples, como bordes verticales, horizontales, o curvas.
• Por ejemplo, la parte superior redondeada de un “3” o la línea vertical de un “1”.

En capas intermedias:

• Se combinan esos patrones simples en formas más complejas, como bucles, arcos y cruces de líneas que componen partes específicas de los números.

En capas más profundas:

• La red empieza a diferenciar entre dígitos completos, aprendiendo las variaciones típicas de escritura que tiene cada número.
• Por ejemplo, entender las diferencias sutiles entre un “4” recto y uno con una curva abierta en la parte superior.

Cada neurona en estas capas aplica una función de activación, como ReLU, que introduce no linealidad, permitiendo que la red aprenda relaciones complejas.

Decisión Final (Capa de Salida)

La última capa tiene 10 neuronas, una por cada dígito posible del 0 al 9. Cada una devuelve una probabilidad (gracias a la función softmax) de que la imagen corresponda a ese número.

Por ejemplo:

Esto significa que la red está 95% segura de que la imagen corresponde al número 2.

¿Por Qué Usar Varias Capas?

• Procesamiento Jerárquico: Cada capa determina algo más complejo que la anterior, desde bordes hasta dígitos completos.
• Generalización: Las redes profundas pueden adaptarse mejor a variaciones de escritura (grosor, inclinación, estilo).
• Modularidad: Caracterizar partes de un número y combinarlas permite que la red reconozca correctamente incluso escrituras no estándar.

Un Ejemplo Paso a Paso

Digamos que la red recibe una imagen con un “8” dibujado a mano:

1. Capa 1: Detecta curvas cerradas arriba y abajo.
2. Capa 2: Reconoce que hay dos bucles conectados verticalmente.
3. Capa 3: Compara esa forma con otras conocidas y concluye que se trata de un «8».
4. Capa de salida: Asigna una probabilidad alta a la clase «8» y lo predice como resultado.

Este proceso se entrena utilizando miles de ejemplos, permitiendo que la red ajuste sus parámetros internos (pesos y sesgos) para maximizar la precisión.

¿Cómo funciona una red neuronal? – No es magia son matemáticas

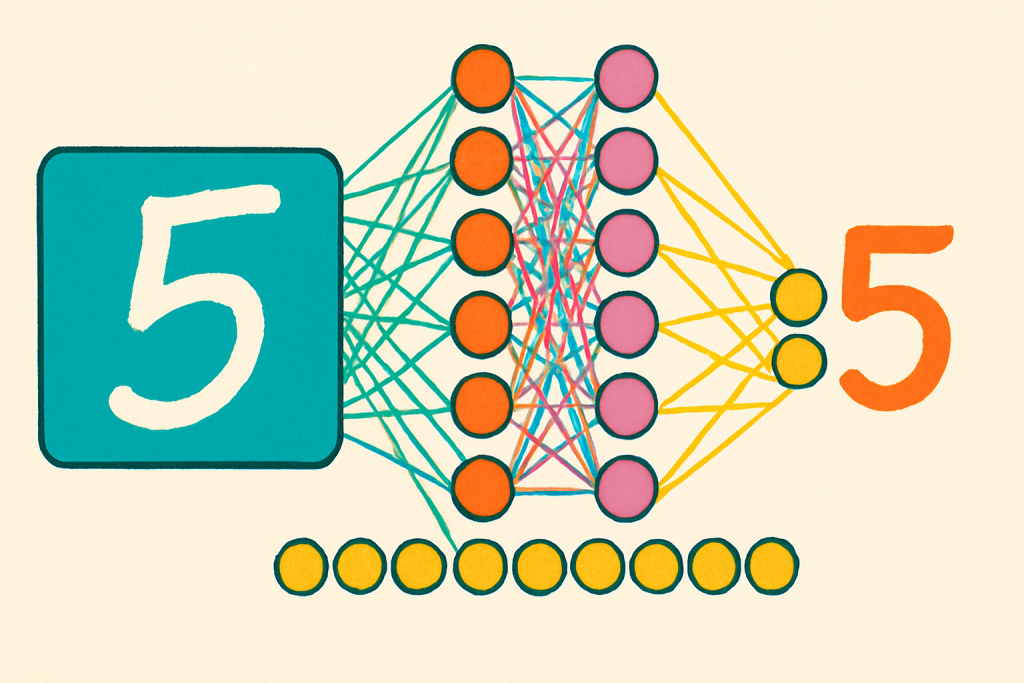
Como hemos hecho hasta ahora en éste tipo de entradas donde intentamos explicar como funciona un algoritmo de IA, a continuación veremos una explicación un poco más técnica en la que usaremos fundamentos matemáticos así como código escrito en Python para explicar como funcionan las redes neuronales.

En el código que encontrarás en éste repositorio, utilizamos la base de datos MNIST (keras.datasets.mnist.load_data()), que contiene imágenes de dígitos escritos a mano del 0 al 9. Cada imagen es de 28×28 píxeles en escala de grises.

Nuestro objetivo es que la red neuronal ajuste sus parámetros para poder diferenciar qué número hay en cada imagen. Veamos cómo lo hace paso a paso.

Paso 1: Transformar imágenes en vectores

Cada imagen tiene dimensiones 28×28, es decir, 784 píxeles. En el paso de preparación de datos (X_train.reshape((60000, 28 * 28))), transformamos cada imagen en un vector de 784 dimensiones.

Desde el punto de vista matemático, podemos representar una imagen como un vector:

Donde cada entrada de ese vector es un número entre 0 y 1 que representa la intensidad de gris del píxel correspondiente.

Paso 2: ¿Qué hace una red neuronal?

Una red neuronal transforma ese vector de entrada a través de capas densas. Cada capa realiza una operación matemática de la forma:

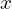• es el vector de entrada.
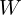• es la matriz de pesos.
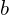• es el vector de sesgo.
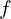• es una función de activación (como ReLU o softmax).
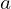• es la salida de la capa.

Estas capas están definidas en el bloque model = keras.Sequential([...]) del código.

Paso 3: Estructura del modelo

En este ejemplo, nuestra red tiene tres capas principales:

model = keras.Sequential([
    layers.Dense(128, activation='relu', input_shape=(28 * 28,)),  # Capa 1
    layers.Dense(64, activation='relu'),                           # Capa 2
    layers.Dense(10, activation='softmax')                         # Capa de salida
])

A nivel matemático, la red aplica tres transformaciones en secuencia:

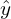• es el vector de salida con las probabilidades para cada clase (dígito del 0 al 9).
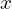• es el vector de entrada (imagen).

Paso 4: Ajuste de parámetros

Durante el entrenamiento (model.fit(...)), la red ajusta sus pesos y sesgos para minimizar una función de pérdida. En este caso usamos:

loss='categorical_crossentropy'

La pérdida de entropía cruzada categórica se define como:

Donde:

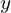• es el vector one-hot de la etiqueta real.
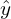• es la predicción del modelo.

El optimizador adam aplica una variante del gradiente descendente para encontrar los mejores valores de los parámetros.

model.compile(optimizer='adam',
              loss='categorical_crossentropy',
              metrics=['accuracy'])

Este proceso se repite en varias iteraciones completas sobre los datos de entrenamiento.

¿Cómo se ajustan los parámetros?

Con el fin de aclarar un poco más esta parte, veámosla en más detalle.

Forward pass (propagación hacia adelante):

• La entrada se propaga a través de la red.
• Se calcula la predicción final.
• Se evalúa la pérdida (error) comparando la predicción con el valor real.

Backward pass (backpropagation):

• Se calculan los gradientes de la función de pérdida con respecto a cada peso de la red, utilizando la regla de la cadena del cálculo diferencial.
• Estos gradientes indican en qué dirección (y cuánto) ajustar cada peso para reducir el error.

Actualización de parámetros:

• Se usan los gradientes calculados para ajustar los pesos, típicamente con un algoritmo como gradient descent o una variante como Adam.

La backpropagation es la fase del «entrenamiento» de una red neuronal en la que el modelo ajusta sus parámetros (pesos y sesgos) para minimizar el error cometido al hacer predicciones.

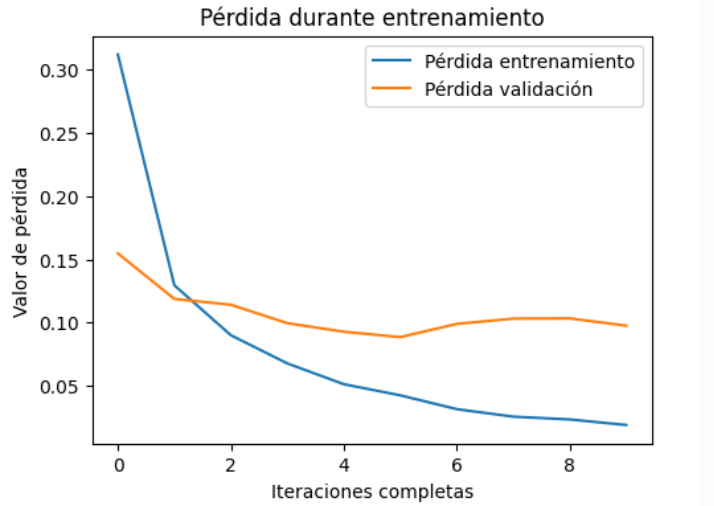
Evolución de la función pérdida

Durante el ajuste de parámetros de una red neuronal, es importante monitorizar tanto el rendimiento sobre los datos con los que se entrena el algoritmo, como sobre un conjunto de validación independiente. En la figura 2 se puede observar cómo la pérdida de entrenamiento disminuye constantemente, lo que indica que la red neuronal está ajustando bien sus parámetros mientras usa el set de datos de entrenamiento. Al mismo tiempo, la pérdida de validación se mantiene relativamente estable, lo cual es una buena señal: significa que el modelo está ajustando sus parámetros de forma eficaz, y no simplemente memorizando los datos.

Paso 5: Evaluación y predicción

Después de ajustar los parámetros, evaluamos el rendimiento del modelo con datos nuevos (model.evaluate(X_test, y_test)) y usamos la red para hacer predicciones:

def predecir_imagen(modelo, imagen):
    imagen = imagen.reshape(1, 784)
    prediccion = modelo.predict(imagen)
    return np.argmax(prediccion)

Este procedimiento aplica las transformaciones descritas anteriormente, y selecciona la clase con mayor probabilidad como predicción final.

Conclusión: El poder y los límites de las redes neuronales

A lo largo de esta entrada, hemos explorado cómo una red neuronal ajusta sus parámetros para reconocer dígitos manuscritos, desde la transformación de imágenes en vectores numéricos hasta la toma de decisiones basada en probabilidades. Aunque su funcionamiento pueda parecer casi «mágico», en realidad se sustenta en un proceso determinista y matemático:

1. Base determinista:
   • Las redes neuronales no «adivinan»: ajustan sus parámetros (pesos y sesgos) mediante algoritmos de optimización (como el descenso de gradiente), minimizando rigurosamente una función de pérdida.
   • Cada predicción es el resultado de operaciones matemáticas bien definidas (transformaciones lineales, funciones de activación como ReLU o softmax).
2. Limitaciones fundamentales:
   • No son universales: Solo resuelven problemas para los que han sido entrenadas. Una red entrenada en MNIST no podrá reconocer letras o objetos complejos sin un reentrenamiento.
   • Dependencia de los datos: Su precisión está ligada a la calidad y diversidad del conjunto de entrenamiento. Si los datos son sesgados o insuficientes, el modelo fallará en casos reales.
3. Potencial y responsabilidad:
   • Estas redes son herramientas poderosas en aplicaciones como procesamiento de imágenes, automatización o asistencia médica, pero su uso requiere entender sus límites.
   • Aunque imitan ciertos aspectos del aprendizaje humano, no comprenden lo que ven; solo detectan patrones estadísticos.

Reflexión final

Las redes neuronales son un ejemplo fascinante de cómo la matemática y la computación pueden emular habilidades humanas en tareas específicas. Sin embargo, su éxito depende de nuestro diseño: la elección de arquitecturas, funciones de pérdida y, en muy gran medida, de los datos de entrenamiento.

«El aprendizaje profundo es como construir un cohete: necesitas un motor potente (el modelo) y mucho combustible (los datos)» – Yann LeCun