In previous posts, we have explored the foundations of artificial intelligence: from the anatomy of algorithms to the workings of artificial neurons and neural networks. We have already described how these systems adjust their parameters based on data, but how do they incorporate uncertainty and adapt their beliefs in the light of new information? This is where Bayes’ Theorem comes into play—a fundamental tool that enables AI systems to “reason” probabilistically.

Before delving into the fascinating world of natural language processing (NLP)—where ambiguity and context are key—it is essential to understand how Bayes provides the mathematical framework for updating knowledge and making decisions under uncertainty. From spam filters to AI-assisted medical diagnostics, this theorem forms the hidden basis of many systems that appear to “think”.

Historical Introduction

Bayes’ Theorem owes its name to Reverend Thomas Bayes (1701–1761), a British statistician and philosopher. Bayes developed this principle to describe how to update the probabilities of hypotheses as new evidence becomes available. However, his work was not widely recognised during his lifetime. It was the mathematician Pierre-Simon Laplace who, years later, refined and popularised the theorem, turning it into a cornerstone of statistics and probability theory.

Today, Bayes’ Theorem is fundamental in fields such as artificial intelligence, machine learning, medicine, and data science, enabling the updating of beliefs in response to observed data.

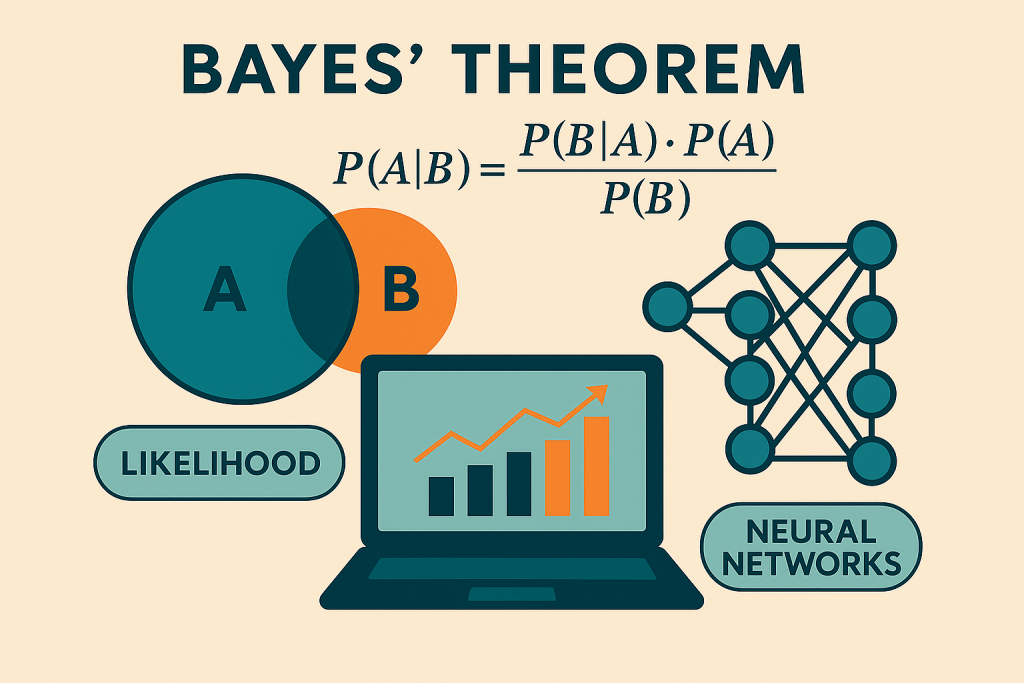
Bayes’ Theorem begins with a simple but powerful question: how should we adjust our expectations when we learn something new?

The theorem provides a rule for updating the probability of a hypothesis H once fresh evidence D comes in.

Here:

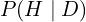• is the posterior probability: probability that is true after observing .
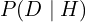• is the likelihood: probability of observing 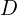if 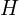were true.
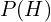• is the prior probability: initial belief (before seeing ).
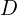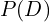• is the evidence or the total probability of observing 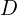, taking into account all possible hypotheses.

Basic application: Email classification

Let us suppose a filtering system analyses whether an email is spam. From a labelled dataset, it calculates:

• The proportion of spam emails (prior probability).
• The frequency with which certain words appear in spam or legitimate emails (likelihood).

When a new email arrives, the model uses Bayes’ Theorem to estimate the probability that it is spam, given the presence of certain words. This process does not involve subjective interpretation: it is a mathematical update based on empirical data.

This is the principle behind Naive Bayes, one of the most widely used classifiers due to its efficiency and simplicity.

The Bayesian approach in machine learning

The Bayesian perspective in machine learning involves treating the parameters of a model as random variables, rather than fixed values. This allows the representation of epistemic uncertainty—that is, uncertainty about what has not yet been learned.

Key Models:

• Naive Bayes: a classifier that assumes conditional independence between predictor variables. Despite its simplicity, it performs surprisingly well in tasks such as text analysis or document classification.
• Bayesian networks: directed acyclic graphs that represent causal or probabilistic dependency relationships between variables. They are useful in medical diagnosis, fault prediction, or modelling complex systems.
• Bayesian neural networks (BNNs): neural networks where the weights are probability distributions. They allow not only predictions but also quantification of the uncertainty of each output.
• Approximate Bayesian inference: such as MCMC sampling or variational inference, techniques used when the exact calculation of the posterior probability is intractable.
• Bayesian optimisation: a strategy that builds a probabilistic model of the search space and uses it to find the best set of hyperparameters with the fewest evaluations.

Advantages of the Bayesian approach

• Mathematical rigour: Bayesian models follow a consistent updating logic, regardless of the domain of application.
• Quantification of uncertainty: not only do they produce a prediction, but also a confidence measure associated with it.
• Natural incorporation of prior knowledge: through the prior distribution, initial learning can be guided, especially useful in settings with scarce data.
• Flexibility: adapts to contexts with complex structures and enables the representation of causal relationships, not just correlations.
• Implicit regularisation: by considering distributions over parameters, overfitting is avoided in a more natural way.

Limitations and challenges

Despite its advantages, the Bayesian approach also presents challenges:

• Computational cost: calculating the posterior distribution is often complex, especially in high-dimensional models.
• Choice of prior: selecting an appropriate prior distribution is not always straightforward and can significantly influence results.
• Scalability: although approximate methods exist, applying Bayesian techniques to very large datasets remains an active research challenge.

Relationship with other currents in AI

Whereas in classical deep learning models tend to search for the parameters that maximise the likelihood of the observed data (maximum likelihood), the Bayesian approach instead models the full distribution of parameters. Rather than a single point estimate, it yields a space of models weighted by their likelihood.

This allows a richer interpretation of results and aligns with approaches such as active parameter tuning, where the system can select examples about which it is most uncertain, or continual parameter tuning, where models are updated without forgetting previously learned knowledge (via cumulative priors).

Conclusion

Bayes’ theory is not simply a technique for calculating conditional probabilities: it is a solid mathematical framework that enables artificial intelligence systems to incorporate data, adapt their inferences, and, above all, explicitly estimate uncertainty. This capability is crucial in contexts where a single prediction is not enough, and it is necessary to understand how reliable that estimate is.

In a world where AI must confront increasingly complex and critical problems, Bayesian methods provide a rigorous foundation for building systems that not only predict, but also calibrate their level of confidence and justify their decisions in a transparent and consistent way.

“The theory of probabilities is nothing but common sense reduced to calculation.”
— Pierre-Simon Laplace