En las próximas entradas voy a intentar explicar como funciona un modelo complejo de inteligencia artificial, para ello iremos de lo más simple; algoritmos de aprendizaje continuo (machine learning, ML en inglés) a lo más complejo, modelos de lenguaje extenso (LLM, por sus siglas en inglés). Esas entradas, formaran parte de la serie: ¿Cómo computan las máquinas?.
Sin más dilación, veamos ¿Qué es? y ¿Cómo funciona? Un algoritmo de aprendizaje automático (ML).
Nota: El código usado para generar los datos incluidos en ésta entrada lo encontrarás en el siguiente repositorio.
¿Qué es un algoritmo de aprendizaje automático?
Un algoritmo de machine learning, o aprendizaje automático, es un conjunto de pasos y reglas que le damos a una computadora para que resuelva un problema. Existen muchos tipos de algoritmos, y la elección del adecuado depende del problema, de los datos disponibles y de la experiencia del analista.
¿Mandarinas o naranjas?
Para entenderlo mejor, imaginemos que queremos diferenciar naranjas de mandarinas usando su diámetro y peso. Aunque para una persona esto pueda parecer sencillo, el objetivo es crear un algoritmo que permita a una computadora separar naranjas de mandarinas de forma automática y autónoma.
Queremos crear un modelo que distinga naranjas de mandarinas usando dos características clave:
- Peso (g): Las naranjas suelen ser más pesadas.
- Diámetro (cm): Las naranjas suelen ser más grandes.
Usaremos Regresión Logística, un algoritmo de clasificación ideal para problemas con dos clases, como en este caso. Luego, visualizaremos la frontera de decisión y evaluaremos la calidad del modelo haciendo uso de la matriz de confusión.
Aprendiendo a Clasificar Frutas con un Algoritmo Supervisado
Para que un modelo de inteligencia artificial aprenda a diferenciar entre naranjas y mandarinas, primero necesitamos datos. Generaremos datos ficticios en los que ambas frutas tengan características ligeramente solapadas, de modo que la tarea de clasificación no sea demasiado sencilla para el algoritmo. Como estamos trabajando con un clasificador supervisado, además de las características como el diámetro y el peso, contaremos con una información clave: la clase de cada fruta, es decir, si es una naranja o una mandarina. Gracias a esto, el algoritmo no ajustará sus parámetros al azar, sino que ajustará sus parámetros identificando patrones en la relación entre las características y las clases.
| # | Clase | Peso (g) | Diámetro (cm) |
| 1 | N | 114.615 | 8.596 |
| 2 | N | 139.483 | 7.834 |
| 3 | N | 141.432 | 8.777 |
| […] | […] | […] | […] |
| 198 | M | 113.846 | 5.367 |
| 199 | M | 77.136 | 5.971 |
| 200 | M | 110.945 | 5.755 |
Separación de los datos
Imaginemos que tenemos un conjunto de datos de naranjas y mandarinas, y queremos construir un modelo de Machine Learning que, basándose en el peso y el diámetro, pueda predecir si una fruta es una naranja o una mandarina. En lugar de utilizar todos los datos para ajustar los parámetros del modelo, los dividimos en dos grupos principales:
Datos de calibración
Es la parte más grande de los datos (generalmente el 70-80%). Éstos datos son usados para ajustar los parámetros del modelo. Es como cuando preparamos un examen resolviendo los problemas del examen del año anterior. Dicho de otra forma, dejamos que el algoritmo vea tanto las características como las clases y de forma iterativa vaya ajustando los parámetros del modelo para minimizar el error en la clasificación.
Datos de prueba
Después de ajustar los parámetros del modelo, probamos la calidad del modelo con éste conjunto de datos (20-30%) para ver cómo se desempeña en datos completamente nuevos no usados previamente durante la fase de ajuste de parámetros del algoritmo. Es como el examen final después de estudiar. En éste caso, sólo mostramos al modelo las características y comparamos el vector de clases que obtenemos como resultado, con el vector de clases reales, que en éste caso hemos ocultado al modelo. Si el modelo tiene un buen desempeño aquí, podemos confiar en que funcionará bien en la práctica.
¿Cómo se ajustan los parámetros del modelo?
Al principio, el algoritmo no tiene conocimiento sobre las frutas. Sin embargo, al recibir los datos de entrenamiento (peso, diámetro y su respectiva etiqueta de naranja o mandarina), empieza a identificar patrones.
Por ejemplo:
- Si una fruta tiene un diámetro grande y un peso elevado, es más probable que sea una naranja.
- Si el diámetro es pequeño y el peso bajo, lo más seguro es que sea una mandarina.
¿Cómo funciona internamente?
Durante el proceso de ajuste de parámetros o entrenamiento, término antropomórfico del que como expliqué anteriormente he decidido rehuir, el modelo modifica sus parámetros para mejorar su precisión, comparando sus predicciones con las clases. Así, va estimando sus parámetros para diferenciar mejor entre naranjas y mandarinas.
En resumen, un modelo supervisado aprende a clasificar objetos mediante ejemplos previamente etiquetados y ajusta sus parámetros para hacer predicciones cada vez más precisas. De esta manera, con suficiente información, podemos ajustar los parámetros de un algoritmo de inteligencia artificial para diferenciar naranjas y mandarinas. Llegados a éste punto me gustaría aclarar que al final del proceso, el algoritmo no sabe que es una naranja ni que es una mandarina. El problema, sin embargo, ha cambiado de forma. El problema ha sido trasladado a un espacio matemático donde hemos visto que la relación de peso y diámetro con naranjas y mandarinas es diferente.
¿Cómo funciona un clasificador? – No es magia son matemáticas
¡Aventurer@ de los números! Nos vamos a adentrar en un territorio donde las matemáticas puede que se compliquen. Pero no entres en pánico, no necesitas un doctorado, solo algo de curiosidad, valentía y, si es necesario, una taza de café bien fuerte. ¡Allá vamos!
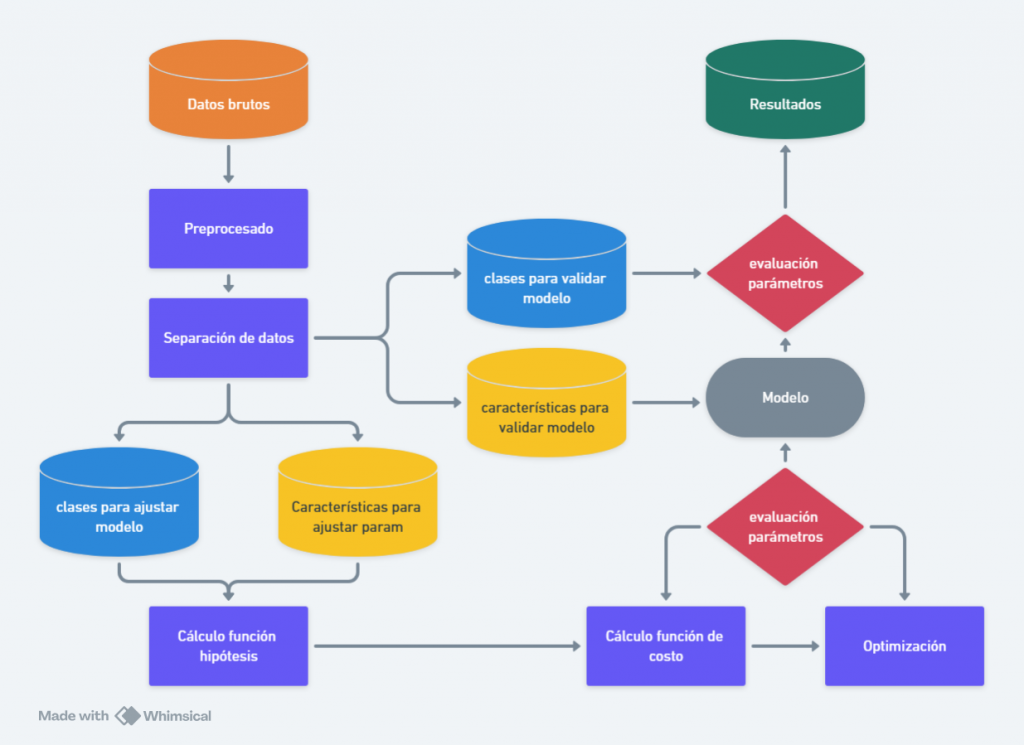
En la figura 2 vemos lo que describo como la anatomía de un algoritmo de ML. El proceso de ML comienza con la recolección y separación de datos. Seguidamente los datos son preprocesados, proceso mediante el cual son limpiados y organizados para su uso. Luego, los datos se dividen en conjuntos de calibración y prueba. Se selecciona un modelo, que ajusta sus parámetros mediante un proceso de optimización. Posteriormente, el modelo se evalúa con los datos de prueba y si es necesario, se ajusta y optimiza para mejorar su desempeño. Finalmente, una vez validado, el modelo se implementa en el mundo real para hacer predicciones y tomar decisiones automatizadas. Veamos ahora con un poco más de detalle matemático, los que a mi opinión son los pasos claves en el desarrollo del algoritmo.
Preprocesamiento de datos
El preprocesamiento de datos es una fase crucial en Machine Learning, donde transformamos los datos crudos en un formato adecuado para ajustar los parámetros del modelo. Este paso incluye limpieza, transformación y normalización de los datos. Aunque hay muchas técnicas de preprocesamiento de datos, en éste caso en particular sólo hemos usado el escalado de datos.
Escalado de datos – Estandarización Z-score
Las características, en nuestro caso peso y diámetro, con escalas muy diferentes pueden afectar el rendimiento del modelo. De hecho, he comprobado que afectan el rendimiento del modelo. Para resolver esto, utilizamos estandarización.
Ésta operación matemática, convierte los valores en términos de desviaciones estándar respecto a la media:
![\[x^{\prime}= \frac{x - \mu}{\sigma}\]](https://ideas-artificiales.es/wp-content/ql-cache/quicklatex.com-49ca900e74553e2bb2ff582433bc34eb_l3.png "Rendered by QuickLaTeX.com")
Donde 
es la media y 
la desviación estándar. Esto centra los datos en 0 con varianza 1.
Función de predicción (hipótesis)
La regresión logística es un modelo utilizado para clasificar datos en dos categorías o clases distintas, generalmente etiquetadas como 0 y 1. Para lograr esto, en lugar de predecir valores continuos como en la regresión lineal, la regresión logística emplea una función especial llamada sigmoide o logística.
![\[\sigma(z) = \frac{1}{1 + e^{-z}}\]](https://ideas-artificiales.es/wp-content/ql-cache/quicklatex.com-a1567ea49ed34acb816ad5e91aa41b6b_l3.png "Rendered by QuickLaTeX.com")
La función de predicción para la regresión logística es:
![\[h_\theta(\mathbf{x}) = \sigma(\mathbf{\theta}^T \mathbf{x}) = \frac{1}{1 + e^{-\mathbf{\theta}^T \mathbf{x}}}\]](https://ideas-artificiales.es/wp-content/ql-cache/quicklatex.com-e1aa3e49c3c31f607d4b4235a49344df_l3.png "Rendered by QuickLaTeX.com")
Donde:
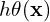es la probabilidad estimada de que la clase sea 1.
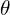es el vector de parámetros (pesos) del modelo.
- Éstos son los famosos parámetros que se ajustan durante el proceso de minimización de costo que veremos más adelante.
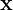es el vector de características de entrada.
- Peso y diámetro.
Interpretación probabilística
La salida de la función sigmoide se interpreta como la probabilidad de que la clase sea 1:
![\[P(y = 1 \mid \mathbf{x}; \theta) = h_\theta(\mathbf{x})\]](https://ideas-artificiales.es/wp-content/ql-cache/quicklatex.com-b8c8864440df4dda18e3f62d320cd506_l3.png "Rendered by QuickLaTeX.com")
Por lo tanto, la probabilidad de que la clase sea 0 es:
![\[P(y = 0 \mid \mathbf{x}; \theta) = 1 - h_\theta(\mathbf{x})\]](https://ideas-artificiales.es/wp-content/ql-cache/quicklatex.com-4e7410d1b3191a44b0d9e3225101758d_l3.png "Rendered by QuickLaTeX.com")
Función de costo
La regresión logística utiliza la función de costo de entropía cruzada (log loss) para medir el error entre las predicciones del modelo y las etiquetas reales. Para un conjunto de datos con m ejemplos, la función de costo es:
![\[J(\theta) = -\frac{1}{m} \sum_{i=1}^m \left[ y^{(i)} \log(h_\theta(\mathbf{x}^{(i)})) + (1 - y^{(i)}) \log(1 - h_\theta(\mathbf{x}^{(i)})) \right]\]](https://ideas-artificiales.es/wp-content/ql-cache/quicklatex.com-92486a17f27374846165a2da5485e450_l3.png "Rendered by QuickLaTeX.com")
Donde:
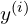es la etiqueta real (0 o 1) para el ejemplo 
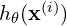es la predicción del modelo para el ejemplo
Optimización del modelo
El objetivo es minimizar la función de costo 
ajustando los parámetros,
. Esto se hace comúnmente usando un algoritmo de minimización conocido como descenso del gradiente. La actualización de los parámetros en cada iteración del descenso de gradiente es:
![\[\theta_j := \theta_j - \alpha \frac{\partial J(\theta)}{\partial \theta_j}\]](https://ideas-artificiales.es/wp-content/ql-cache/quicklatex.com-8c0dd60a3a8bd514bfb6ce61a97e5208_l3.png "Rendered by QuickLaTeX.com")
Donde:
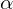es la tasa de aprendizaje.
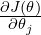es la derivada parcial de la función de costo con respecto a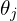 
Por lo tanto, la regla de actualización de los parámetros es:
![\[\theta_j := \theta_j - \alpha \frac{1}{m} \sum_{i=1}^m \left( h_\theta(\mathbf{x}^{(i)}) - y^{(i)} \right) x_j^{(i)}\]](https://ideas-artificiales.es/wp-content/ql-cache/quicklatex.com-a8af23fe98ea791c155a6fac0dba66a5_l3.png "Rendered by QuickLaTeX.com")
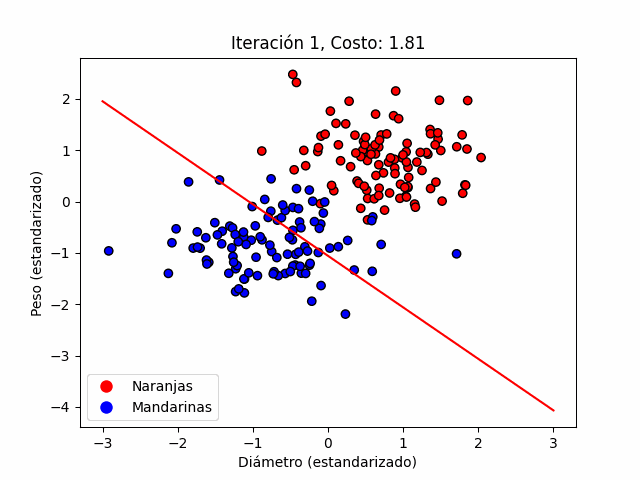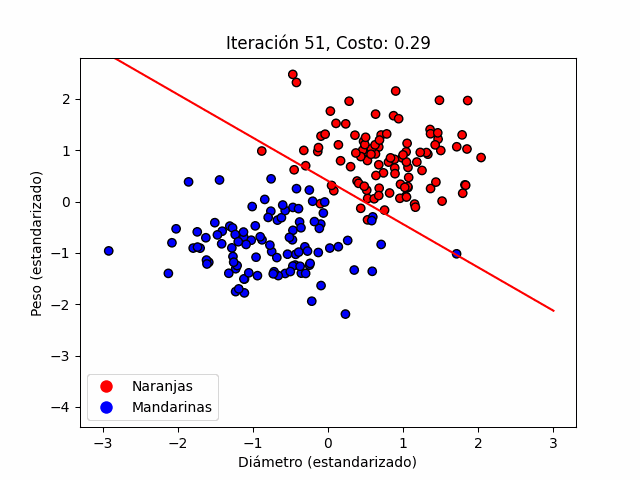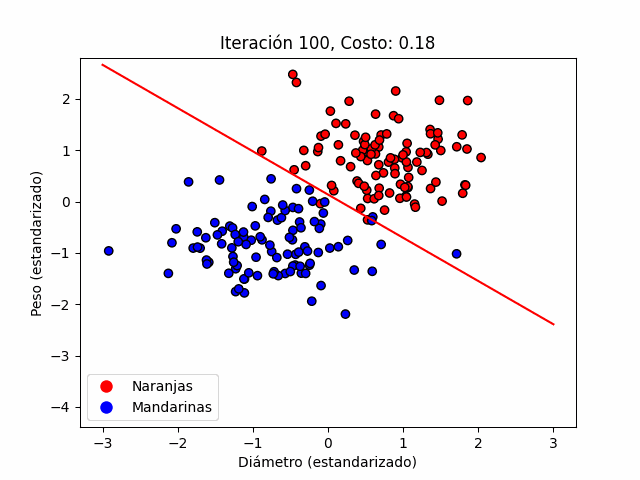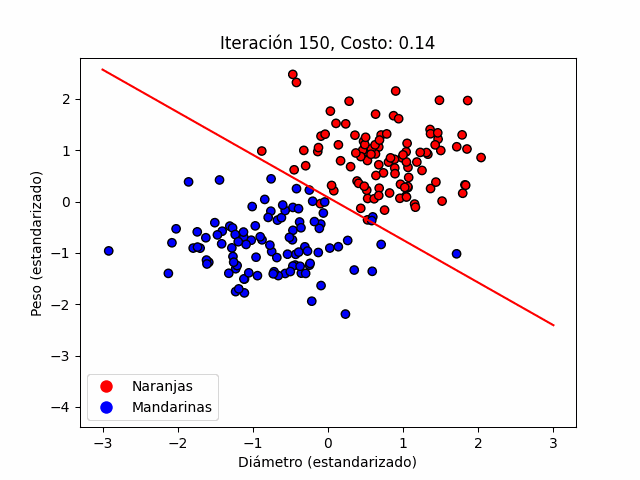
La figura 3 ilustra el proceso iterativo descrito en la ecuación anterior. Podemos ver como la frontera de decisión se mueve como consecuencia de un proceso de minimización de la función de costo. Éste proceso, como hemos visto, se hace en función de los parámetros. Ésta figura es generada en la primera celda del jupyter notebook que encontrarás en éste enlace.
Permitidme enfatizar, aquí el algoritmo no aprende nada, tan sólo procesa de forma iterativa una minimización.
Una vez entrenado el modelo, se puede utilizar para clasificar frutas que no pertenezcan al set de datos de calibración. Dado un vector de características , se calcula 
y se asigna la clase de la siguiente manera:
![\[\text{Clase} =\begin{cases}1 & \text{si } h_\theta(\mathbf{x}) \geq 0.5 \\0 & \text{si } h_\theta(\mathbf{x}) < 0.5\end{cases}\]](https://ideas-artificiales.es/wp-content/ql-cache/quicklatex.com-ac588d52c95926d94e739e19f6fac572_l3.png "Rendered by QuickLaTeX.com")
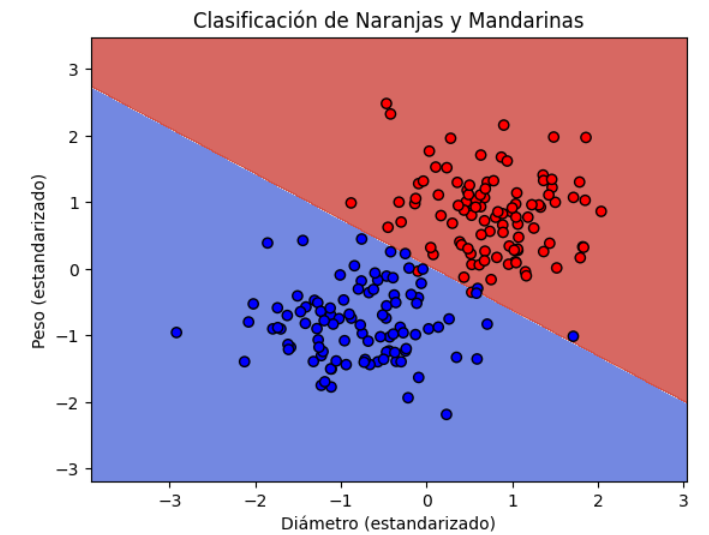
En la figura 4 podemos ver como, al final del proceso iterativo, el espacio característico queda dividido en dos partes. Éste es el resultado final del ajuste de parámetros del modelo, una vez obtenida la frontera de decisión y la separación del espacio característico, cualquier nueva fruta que no pertenezca al set de datos usado para el ajuste de los parámetros puede ser clasificada. Ésta figura es generada en la segunda celda del jupyter notebook que encontrarás en éste enlace.
De hecho, ese último paso se lo tenemos reservado a los datos de prueba que hasta ahora no hemos usado.
Evaluación del modelo
Una vez ajustados los parámetros y definida la frontera de decisión, es fundamental evaluar el rendimiento del modelo para determinar su efectividad. Una de las herramientas más utilizadas para esta evaluación es la matriz de confusión, que proporciona un desglose detallado de los aciertos y errores del modelo.
La matriz de confusión, que por cierto vaya nombrecito, es una tabla que compara las predicciones del modelo con los valores reales. Para nuestro problema en concreto, la matriz sería la siguiente:
| Naranja predicha | Mandarina predicha | |
| Naranja real | TP | FN |
| Mandarina real | FP | TN |
Donde:
- TP (True Positives): Frutas correctamente clasificados como Naranjas.
- TN (True Negatives): Frutas correctamente clasificados como Mandarinas.
- FP (False Positives): Frutas incorrectamente clasificados como Naranjas (error tipo I).
- FN (False Negatives): Frutas incorrectamente clasificados como Mandarinas (error tipo II).
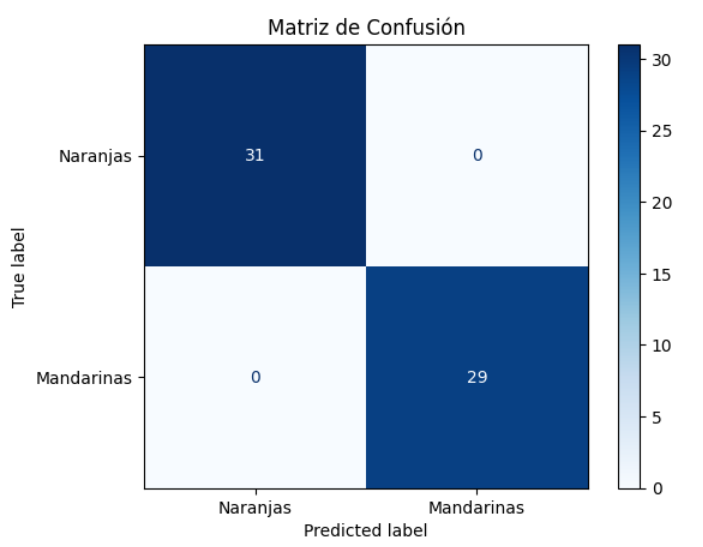
En éste caso podemos ver que todas las naranjas y mandarinas pertenecientes a los datos de validación han sido correctamente clasificadas. No tenemos ni falsos positivos ni falsos negativos. Ésta figura es generada en la segunda celda del jupyter notebook que encontrarás en éste enlace.
Por tanto, podemos decir que el algoritmo está listo para ser instalado en las computadoras encargadas de separar naranjas de mandarinas basándose en el peso y el diámetro de las mismas.
Conclusiones
En ésta entrada hemos visto como funciona un algoritmo de aprendizaje automático supervisado desde un punto de vista divulgativo y de forma un poco más profunda. En mi opinión hay algo realmente brillante detrás de cualquier clasificador supervisado. Para mi, la brillantez radica en la transformación del problema, sea cual sea su naturaleza, a un problema de minimización de errores, en otras palabras, un problema de distancias. Al fin y al cabo, la optimización de parámetros del modelo se lleva a cabo en base a una minimización de error. El error de clasificación de las clases derivadas de las características de los datos de entrenamiento, tras pasar por el modelo, con respecto a las clases conocidas, ya que recordemos estamos tratando con modelos supervisados.
El algoritmo no aprende, solo sigue pasos.
No es magia, son matemáticas.
