En entradas anteriores, hemos explorado los cimientos de la inteligencia artificial: desde la anatomía de los algoritmos hasta el funcionamiento de las neuronas artificiales y las redes neuronales. Estos sistemas ajustan sus parámetros a partir de datos, pero ¿ cómo incorporan la incertidumbre y adaptan sus creencias frente a nueva información? Aquí es donde entra en juego el Teorema de Bayes, una herramienta fundamental que permite a los sistemas de IA «razonar» probabilísticamente.

Antes de adentrarnos en el fascinante mundo del procesamiento del lenguaje natural (PLN) —donde la ambigüedad y el contexto son clave—, es esencial entender cómo Bayes proporciona el marco matemático para actualizar conocimientos y tomar decisiones bajo incertidumbre. Desde los filtros de spam hasta los diagnósticos médicos asistidos por IA, este teorema es la base oculta detrás de muchos sistemas que parecen «pensar».

Introducción Histórica

El Teorema de Bayes debe su nombre al reverendo Thomas Bayes (1701–1761), un estadístico y filósofo británico. Bayes desarrolló este principio para describir cómo actualizar las probabilidades de las hipótesis a medida que se obtiene nueva evidencia. Sin embargo, su trabajo no fue ampliamente reconocido durante su vida. Fue el matemático Pierre-Simon Laplace quien, años más tarde, refinó y popularizó el teorema, convirtiéndolo en un pilar de la estadística y la teoría de la probabilidad.

Hoy, el Teorema de Bayes es fundamental en campos como la inteligencia artificial, el aprendizaje automático, la medicina y la ciencia de datos, permitiendo actualizar creencias en función de datos observados.

Enunciado del teorema

La teoría de Bayes parte de una pregunta fundamental: ¿cómo debería cambiar una estimación probabilística cuando se dispone de nueva información?

El Teorema de Bayes responde a esta pregunta mediante una regla que permite actualizar la probabilidad de una hipótesis , dada una observación :

Aquí:

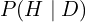• es la probabilidad posterior: la probabilidad de que H sea cierta después de observar D.
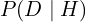• es la verosimilitud: la probabilidad de observar D si H fuera cierta.
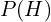• es la probabilidad previa: la creencia inicial (antes de ver D).
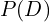• es la evidencia o probabilidad total de observar D, considerando todas las posibles hipótesis.

Aplicación Básica: Clasificación de Correos

Supongamos que un sistema de filtrado analiza si un correo es spam. A partir de un conjunto de correos etiquetados, calcula:

• La proporción de correos spam (probabilidad previa).
• La frecuencia con que aparecen ciertas palabras en correos spam o legítimos (verosimilitud).

Cuando llega un nuevo correo, el modelo usa el Teorema de Bayes para estimar la probabilidad de que sea spam, dada la presencia de ciertas palabras. Este proceso no implica interpretación subjetiva: es una actualización matemática basada en datos empíricos.

Este es el principio detrás del Naive Bayes, uno de los clasificadores más utilizados por su eficiencia y simplicidad.

El Enfoque Bayesiano en Machine Learning

La perspectiva bayesiana en machine learning consiste en tratar los parámetros de un modelo como variables aleatorias, no como valores fijos. Esto permite representar incertidumbre epistemológica, es decir, incertidumbre sobre lo que aún no se ha aprendido.

Modelos Clave:

• Naive Bayes: clasificador que asume independencia condicional entre variables predictoras. A pesar de su simplicidad, funciona sorprendentemente bien en problemas como análisis de texto o clasificación de documentos.
• Redes Bayesianas: grafos dirigidos acíclicos que representan relaciones causales o de dependencia probabilística entre variables. Son útiles en diagnóstico médico, predicción de fallos, o modelado de sistemas complejos.
• Bayesian Neural Networks (BNNs): redes neuronales en las que los pesos son distribuciones de probabilidad. Permiten no solo hacer predicciones, sino cuantificar la incertidumbre de cada salida.
• Inferencia Bayesiana Aproximada: como el muestreo MCMC o la inferencia variacional, técnicas utilizadas cuando el cálculo exacto de la probabilidad posterior es intratable.
• Optimización Bayesiana: estrategia que construye un modelo probabilístico del espacio de búsqueda y lo utiliza para encontrar el mejor conjunto de hiperparámetros con el menor número de evaluaciones.

Ventajas del Enfoque Bayesiano

1. Rigor Matemático: los modelos bayesianos siguen una lógica de actualización coherente, independientemente del dominio de aplicación.
2. Cuantificación de la Incertidumbre: no solo se obtiene una predicción, sino también una medida de confianza asociada.
3. Incorporación Natural de Conocimiento Previo: a través de la distribución previa, se puede guiar el aprendizaje inicial, especialmente útil en entornos con pocos datos.
4. Flexibilidad: se adapta a contextos con estructuras complejas y permite representar relaciones causales, no solo correlaciones.
5. Regularización Implícita: al considerar distribuciones sobre parámetros, se evita el sobreajuste de forma más natural.

Limitaciones y Retos

A pesar de sus ventajas, el enfoque bayesiano también presenta desafíos:

• Coste Computacional: calcular la distribución posterior suele ser complejo, especialmente en modelos de alta dimensión.
• Selección de Prior: elegir una distribución previa adecuada no siempre es trivial y puede influir significativamente en los resultados.
• Escalabilidad: aunque existen métodos aproximados, aplicar técnicas bayesianas en grandes volúmenes de datos sigue siendo un reto activo de investigación.

Relación con Otras Corrientes de IA

Mientras que en el aprendizaje profundo clásico los modelos tienden a buscar los parámetros que maximizan la probabilidad de los datos observados (maximum likelihood), el enfoque bayesiano opta por modelar la distribución completa de parámetros. En lugar de un único modelo puntual, se obtiene un espacio de modelos ponderado por su verosimilitud.

Esto permite una interpretación más rica de los resultados y se alinea con enfoques como el ajuste de parámetros activo, donde el sistema puede seleccionar ejemplos sobre los que tiene mayor incertidumbre, o el ajuste de parámetros continuo, donde se actualizan los modelos sin olvidar lo aprendido previamente (mediante priors acumulativos).

Conclusión

La teoría de Bayes no es simplemente una técnica para calcular probabilidades condicionales: es un marco matemático sólido que permite a los sistemas de inteligencia artificial incorporar datos, adaptar sus inferencias y, sobre todo, estimar la incertidumbre de manera explícita. Esta capacidad es crucial en entornos donde no basta con una predicción puntual, sino que se requiere entender cuán confiable es esa estimación.

En un contexto donde la IA debe enfrentar problemas cada vez más complejos y críticos, los métodos bayesianos ofrecen una base rigurosa para construir sistemas que no solo predigan, sino que también calibren su nivel de confianza y justifiquen sus decisiones de forma transparente y coherente.

“La teoría de las probabilidades no es otra cosa que el sentido común reducido a cálculo.”
— Pierre-Simon Laplace